page 53
Part 2: Section 1 - The Rise of Modern Science
THE FAMOUS CONFLICT BETWEEN SCIENCE AND RELIGION IS commonly thought of in terms of supposed contradictions beetween particular dogmas of religion and particular discoveries of science. Thus the discoveries of geology shattered the belief that the world was created in six days a few thousand years ago. The Darwinian theory of evolution showed that man is not a special creation unrelated to the animal kingdom. The application of scientific techniques of historical and literary criticism to the Bible proved that that book is not a literal record of facts dictated by God. A long history of scientific discoveries of this kind prooduced a series of shocks in the domain of Christian belief.
While it cannot be doubted that these shocks have had a powerful effect in the way of undermining religious faith, it must be pointed out that this is on the whole a very superficial account of the conflict between religion and science. The real antagonism lies much deeper. It is not between particular discoveries of science and particular dogmas of religion at all. It is rather that certain very general assumptions which are implicit in the scientific view of the world conflict with basic assumptions of the religious view—any religious view, not merely the Christian view —of the world. For instance, it is part of the religious view that the world is a moral order. Now the denial of this, the assertion
page 54
that the world is not a moral order, is not, of course, a "discovery" of any particular science. It does not belong to physics or astronnomy or botany. It is not even part of the general body of science, and no scientific man would be thought "unscientific" for denying it. It is not a scientific problem at all. It is a philosophical probblem. How then can it be in any way fathered upon science? We are not yet ready to answer this question. That there is some connection is certain. But before we can say what it is we must have before us some account of the origins of modern science and its implications.
If we were concerned with the difficulties raised for religion by particular scientific discoveries, we should have to concentrate on comparatively recent science, particularly that of the nineeteenth century. It was then that the new geology and the theory of evolution broke upon the world. But the general scientific attitude, the basic assumptions of the scientific view of the world—which have been the real enemies of religious faith—were rather the work of men such as Kepler and Galileo. The program of the whole scientific movement of the modern world, the presuppositions upon which it has been built, were complete by the time Newton had done his work. In so far as we are to consider science as the builder of the modern mind, it is the early scientists whom we have to study, not Lyell or Darwin, much less Einstein or Niels Bohr. It was the founders of science in the seventeenth century who produced the violent change from the climate of opinion of the medieval period to the climate of opinion of the modern period, some of the characteristics of which we have already examined. Those special discoveries of science which have seemed to conflict with special Christian dogmas came mostly in the nineteenth century. Yet the great age of religious skepticism was the eighteenth century, immediately following the birth of modern science. The nineteenth century was by comparison almost a return to an age of faith. For the romanticism which dominated it was essentially a religious reaction against skepticism. The modern mind is the product of seventeenth century science, not of that of the nineteenth century much less of twenti-
page 55
eth century science. For this reason I shall devote the present chapter to a brief factual account of the seventeenth century scientific revolution.
Copernicus (1473-1543) lived a full century before the period which is properly denominated the seventeenth century scientific revolution. Yet that revolution would have been impossible without him, and it built upon his theories. Extracts from his book, De revolutionibus orbium coelestium, were published as early as 1530, but the full text did not appear until 1543, the year in which he died.
His great achievement, as everyone knows, was to replace the geocentric by the heliocentric theory of astronomy. In crude terms this means that the earth goes round the sun, not the sun round the earth. The geocentric theory, which had been taken for granted since ancient times, had been elaborated into a mathematical system by the Alexandrian astronomer Ptolemy in the second century of our era. The Ptolemaic system was built upon three basic assumptions: first, that the earth rests immovable at the center of the universe; second, that all the heavenly bodies revolve around it; third, that their orbits round the earth are circular.
While the first two of these assumptions caused no difficulties, the third conflicts with plain facts which were well known even to the ancients. It had been known from ancient times that the planets "wander" in the sky. For instance, if Jupiter is watched throughout the year it will be observed that, in addition to its daily revolution round the earth along with the stars, it has an annual movement relative to the stars which is a kind of loop, roughly like this:

That is, it moves among the stars from west to east, turns backwards in a "retrograde" movement from B to A, and then
page 56
resumes its eastward march. It traverses the loop in a period of some months. In the following year it loops the loop again, but not in the same region of the sky. The loops themselves move round the sky returning to roughly the same region after about twelve years. Thus the movement among the stars over the period of twelve years looks something like this:
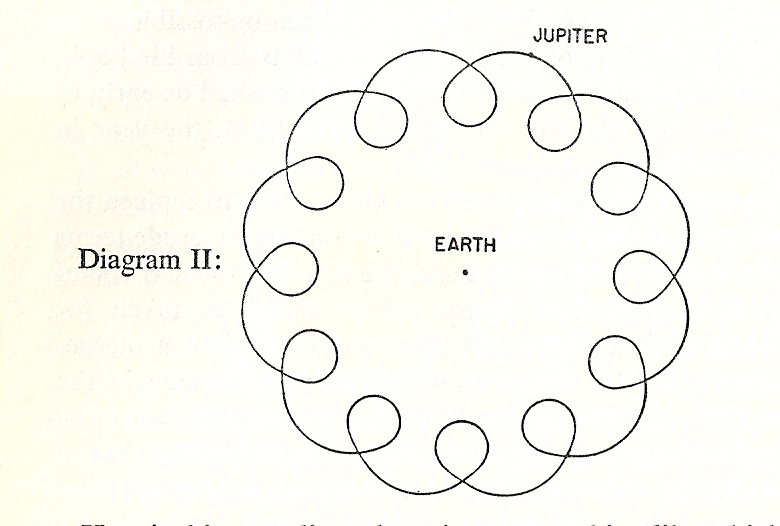
How is this complicated motion—something like which occurs in all the planets, and not only Jupiter—to be made consistent with the view that they move in circles round the earth as center?
The explanation of this was the great feat of Ptolemy's astronnomy. He accounted for it by an ingenious theory of "epicycles." Suppose that on the rim of a wheel another wheel, which we will call an epicycle, is centered, as in the diagram:

Then if both wheels rotate round their centers, a point on the rim of the epicycle, such as P, will perform an evolution similar to that of Jupiter as shown in Diagram II.
page 57
But suppose that the observed motions of a planet cannot be exactly explained by a circle and one epicycle, it may be that a circle and two epicycles, or even more, can be arranged so that the movement of the point P will exactly correspond to the moveement of the planet, as thus:
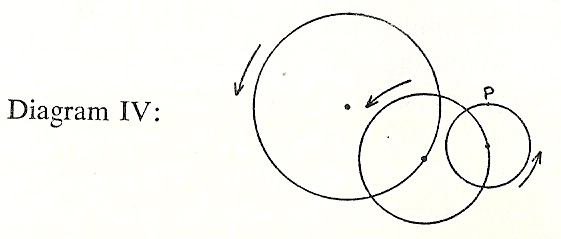
There is no end to the possible detailed elaborations of such an idea, and it is obvious that, with sufficient mathematical ingenuity, almost any wandering movement in the sky, provided it returns upon itself, can be explained in terms of nothing but circles. Great care will have to be taken to get the diameters of each of the circles right, and also the velocities of their rotations. But this is what the Ptolemaic system achieved for each of the heavenly bodies. It was done with sufficient accuracy to enable astronomers to make at least rough predictions about their posiitions in the heavens at future dates.
The great disadvantage of the system was its cumbersome and complicated character. No less than seven circles and eighty epicycles were found necessary to explain the movements of the known bodies of the solar system.
An interesting sidelight on the history and characteristics of human thought appears in connection with the question why the Ptolemaic astronomers thought it necessary to construct the actually non-circular observed motions of the planets out of fictitious circles. Why were they obsessed with the idea of the circle? Why did not Ptolemy simply say that Jupiter in fact moved round the earth in the eccentric course shown in Diagram II? Why should it not? Why must it be pretended that only circles are involved?
The question is complicated by the fact that the ancients be-
page 58
lieved that the heavenly bodies are fixed on to solid revolving spheres. If this were so, then he epicycle might be real. But if there were no such revolving spheres, if the planets moved in empty space, then the epicycles would be mere fictions, imaginary circles out of which the actually eccentric motions of the planets were constructed. They would be no more than mathematical dodges. Ptolemaic writers appear to have held both views. But whatever was the truth about the solid spheres, there is no doubt that this was not the only explanation why the Ptolemaic astronomers thought that all planetary paths must be somehow made out to be circular. There was another cause at work.
The Greeks, including Plato, supposed that the heavenly bodies are divine beings. They also thought that the circle is the only "perfect" figure. Therefore, since the heavenly bodies are divine, their motions must be perfect, that is to say, circular. It is not to be supposed that the Ptolemaic astronomers believed exactly this. But this belief of the Greeks produced in the western world a reverence for circles which obstructed astronomy for about two thousand years.
What exactly did Copernicus accomplish? The essence of his contribution to science lay in the brilliant insight that the loop-like motions of the planets could be explained, in a much simpler manner than that employed by Ptolemy, if the assumption were made that the planets revolve round the sun, and that the earth itself is a planet which revolves round the sun while at the same time it rotates daily on its axis. Copernicus proved that if this assumption were made, he could dispense with most of Ptolemy's epicycles, and thus greatly simplify astronomical calculations. The exact point will be made clear by looking at the diagram:
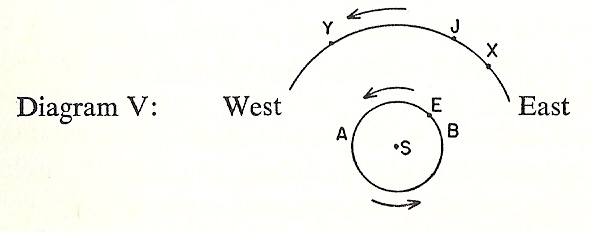
page 59
Suppose that the earth revolves around the sun in one ye~ as shown by the arrows, and that Jupiter moves round the sun m a little over twelve years. In one year, then, Jupiter will move through an arc of a circle, say XY. Then when the earth is moving on the lower half of its circle from west to east, Jupiter will appear from the earth to be travelling rapidly from east to west. But when the earth is moving on the upper half of its circle from east to west, it will catch up and pass Jupiter, so that Jupiter will appear to an observer on the earth to have reversed its direction and to be travelling backwards from west to east. It will appear to be travelling backwards for the same reason as a train moving west at thirty miles an hour will, as seen by an observer on another train which passes the first on a parallel track at sixty mIles an hour, appear to be travelling backwards. This explains why Jupiter is seen to be moving from east to west during part of the year, and then appears to reverse itself into a retrograde movement from west to east during the rest of the year. Thus we can get rid of the epicycles and explain the observed facts by merely having two circles, one for Jupiter and one for the earth. The same principle can be applied to the other planets .
One might naturally suppose that in this way Copernicus could have got rid of all Ptolemy's epicycles and be left with nothing but the sun in the middle and one circle for each planet. As a matter of fact he could not do this. But he greatly reduced the number of epicycles. Ptolemy had to assume eighty epicycles. Copernicus got rid of forty-six, but was left with thirty-four. The reasons for this are complicated. But one reason was that Copernicus still assumed that the orbits of the planets must be at least roughly circular. They are, in fact, elliptical, as Kepler afterwards showed. Hence the actual ellipses had still to be explained by Copernicus in terms of epicycles. But he did get rid of those epicycles by which Ptolemy had explamed the loop-like motions of the planets.
By reducing the number of epicycles from eighty to thirty-four, Copernicus greatly simplified the calculatlons necessary in the astronomy of the solar system. This greater simplicity is the only
page 60
way in which the Copernican system is superior to the Ptolemaic. It is not any "truer." It is only more convenient, because simpler. Copernicus dId not dIscover a single new fact about the universe. He made no observations on the nature or movements of the heavenly bodies which had not been made before. He did not, for instance, observe a new planet or a new comet. He thus discovered no new facts. What he did was to arrange the already known facts in a new and simpler way. That the heliocentric theory is not truer, but only more convenient, than the geocentric theory, folllows at once from the principle of the relativity of motion. Supppose that there were only two bodies, A and B, in the universe, and that they were, at a given time, ten miles apart; and that five minutes later they were observed to be only five miles apart. Motion has taken place. But which of the two bodies has moved or have they both moved? There is obviously no possible way in which this question could be answered. No measurement or observation could throw any light on it. Thus it would make no difference at all which body you say has moved. You could assume, if you like, that A has remained at rest, and that B has moved towards it at a velocity of a mile a minute. Or you could assume that B was at rest and that A moved at a velocity of a mile a minute. Or you could assume that they both moved, A at twenty rmles an hour and B at forty miles an hour; or A at fifty miles an hour and B at ten miles an hour; and so on. Since there would be no facts against which you could check these assumptions so as to say which is correct, it follows that no one of them is more "true" than the others. But it is possible that one might be more convenient than the others. For instance, it might be easier to assume that only one of the bodies had moved, and not both. But any of the different hypotheses would equally well explain the observed fact, namely, the diminution of the distance between A and B. Exactly the same principle will hold if the number of bodies in the universe is three, or thirty, or a billion, instead of two. You can take any one body as your center of reference, consider it at rest, and suppose that all the other bodies are moving relatively to it. Thus it is no truer to say that the sun is at rest and that the earth goes round it than it is to say the opposite. But
page 61
Copernicus proved that it is mathematically much simpler to take the sun as the center, since it gets rid of a lot of complicated calculations about epicycles. Hence if anyone today likes to be an eccentric individualist and to assert that he still believes that the sun goes round the motionless earth, there will be nobody who can prove him wrong—a way of defending the medieval view which unfortunately did not occur to the Pope and the inquisition who condemned Galileo as heretical for accepting the heliocentric theory.
It is sometimes said that although Copernicus did not prove his theory to be true, this was later proved by Newton, and further confirmed by later discoveries such as that of stellar parallaxes. This is not strictly correct. All it means is that Newton found it convenient to base his law of gravitation on the Copernican view, and that this procedure proved enormously successful. But it would still be logically possible to assume the Ptolemaic view, and to account on the basis of it for all the facts of astronomy and physics known up to date. One can go further and say that no fact which could be observed in the future could ever conceIvably contradict it. The only trouble is that if we were now to assume the truth of the Ptolemaic view, we should have to rewrite the whole of science to fit the assumption, including of course Newton's law of gravitation, not to mention Einstein's; that this new version of science would be almost inconceivably complicated; that this would be very inconvenient; and that it seems therefore better on the whole to "believe in" the Copernican theory.
It must not be supposed that the heliocentric theory, as soon as it was proposed by Copernicus, gained ascendancy. It took over a century before it came to be generally accepted even by men of science. It was still in doubt even in Galileo's time a hundred years later. The great Danish astronomer Tycho Brahe, who flourished roughly half a century after Copernicus, stIll insisted that the earth is at rest with the sun moving around it, although he followed the new theory to the extent of believing that some of the planets move round the sun-a curious comproomise between the Ptolemaic and the Copernican hypotheses which found considerable favor at the time. It will be noted, of course,
page 62
that this compromise theory is, in view of the principle of the relativity of motion, a perfectly defensible hypothesis, as "true' as either of the two hypotheses between which it mediates. Even Galileo accepted the heliocentric theory only after hesitation. It then became a matter of furious controversy between science and the Church. Galileo finally put it on the scientific map, though he suffered imprisonment at the hands of the Inquisition for doing so.
Tycho Brahe (1546-1601) is a transitional figure. His contribution to science does not lie in his compromise between the two theories of astronomy, or in any other theoretical advance—his gifts were not those of the theoretician—but in the practical business of observation. He built the first astronomical observatory. He invented the quadrant for measuring the altitudes of the heavenly bodies above the horizon, and the sextant for measuring the angular distances between them. The telescope not having been invented, his observations were made with the naked eye. He spent his life making and recording in tables the positions of the planets in the sky at specific dates and times—that is to say, in plotting their paths. He did this with a degree of accuracy previously unknown. He reduced the previous margin of error from ten minutes of arc to half a minute, i.e., to one one-hundred-and-twentieth of a degree. His tables and observations constituted the data on which Kepler and Newton afterwards built their theoretical constructions, and their work could not have been done without his prior spadework. He may be called the father of accurate measurement in astronomy.
Kepler (1571-1630) brought to science gifts which were the opposite of Tycho's. He was not a skilled observer, but a great theoretician. He made use of Tycho's observations. His great discovery was that the planets move in ellipses, not in circles. He established three laws of planetary motion. The first was that the planets move in elliptical orbits with the sun in one focus, the other focus being empty. The second law, that each planet sweeps out equal areas in equal times, established a mathematical formula which correlated the velocity of a planet at a given point in its orbit with its distance from the sun at that point. The third law stated that the square of the time of a planet's revolution in its orbit is proportional to the cube of its mean distance from the sun. Given these three laws, the position of a planet in the sky at any time can be predicted without recourse to any theory of epicycles. What enabled Kepler to get rid of the epicycles which were still left in the astronomy of Copernicus was his substitution of ellipses for circles. Thus he completed the simplificaation of astronomical theory which had begun with Copernicus.
Kepler's work is revolutionary in that he broke finally with the superstitious awe in which the circle as the perfect figure had been held. And his work is marked also by one of the outstanding characteristics by which modern science is distinguished from medieval and Greek science. Whereas the ancients and the medieval writers tended to argue a priori from assumed first principles that the truth must be so and so, modern science is based upon the belief that the only way to discover truth is to look at the facts. If you want to know whether there are oak trees in the Congo, you cannot find this out by sitting in an armchair in New York and arguing from some a priori axiom that there must be oak trees there, or that there cannot be any. You have to look at the facts, which in this case would mean going to the Congo to see. This seems obvious to us now, but it is only modern science which has made it obvious. The argument that the planets must move in circles because that is the perfect figure was an example of the opposite procedure. But Kepler, by looking at the facts (as observed by Tycho Brahe)—which in this case meant observing the actual paths of the planets in the sky—discovered that the planets move in elliptical orbits.
Galileo (1564-1642) is famous for so many discoveries that we must here pass over most of them with a bare mention in order to concentrate on the one which is most important to our story—which concerned the laws of motion.
He constructed the first astronomical telescope. Turning it upon the moon, he discovered that that body is not a perfect sphere, but is wrinkled by mountains and valleys. This was a nail in the coffin of the medieval view of the world because it had always been supposed that the heavenly bodies must be perfect
page 64
spheres for the same reason as their orbits must be perfect circles; the sphere being the only perfect solid figure. The existence of mountains and valleys on the moon also made it probable that the moon is composed of the same sort of gross matter as the earth, whereas the medieval view was that the earth alone is made of crude matter, while the heavenly bodies, being nearer the divine, are composed of a special ethereal or semi-divine substance.
Galileo observed with his telescope many new stars invisible to the naked eye. He made the famous discovery of four of the satellites of Jupiter. This raised a storm because it suggested that the earth with its moon might very likely be a planet moving round the sun, like Jupiter. Accordingly learned men refused Galileo's invitation to look through his telescope and see Jupiter's satellites for themselves, lest their faith in religion should be corrrupted. One critic made the comment that these satellites are invisible to the naked eye, and can exert no influence on the earth, and that they are therefore useless, and consequently cannnot exist. This remark is not merely funny, as it may seem to us. It brings to a sharp focus a fundamental contrast between the medieval mind and the modern mind. For it is based upon the premise that what is not useful for some purpose cannot exist, which expresses in a sentence the assumption of the teleological character of the universe. If it seems funny to us, this is because we no longer believe that whatever exists must serve some purpose, because, in fact, we have lost faith in a world-purpose. The incident also illustrates the medieval habit of arguing from a priori principles that the truth must be so and so, whereas Galileo, embodying the spirit of modern science, looked at the facts. The whole clash of the medieval and the modern thus appears in this incident.
But the great discovery of Galileo on which attention should here be concentrated was the first law of motion. This was not indeed very clearly stated by Galileo. It received explicit formulation in the work of Newton. Nevertheless Galileo was the first to understand it. If you push a cart along a rough road, and then stop pushing, the cart soon slows down and stops. If your automobile is running at fifty miles an hour, and you turn off the
page 65
engine the automobile likewise slows down and comes to a standstill. To keep the cart or the automobile running at a uniform speed, you have to keep on applying a force to it. All ordinary observations of moving bodies seem to prove the rule that a force of some kind is required to keep a body moving. This was supposed by Aristotle to be a law of nature: and was accepted as such throughout the middle ages until the time of Galileo. The same law was applied to the planets and stars. They are in continual motion in the sky. Therefore some force must be pushing or pulling them. A popular belief was that spirits or angels carry them along. Even scientific men made the same assumption that a moving force is required. Thus Descartes suggested that space is full of whirlpools of ether which carry the planets round and round, as the force of the water in an eddy will carry floating objects round with it.
The first law of motion tells us, to the contrary, that no force is required to keep an object moving with a uniform velocity. It states that a body continues indefinitely in its state of rest, or of uniform motion in a straight line, unless some force acts upon it. So far as the condition of a body at rest is concerned, this agrees with common sense. If a body is at rest, it will remain at rest indefinitely unless some force pushes or pulls it from its place. This is what everybody would suppose. But what the law states about a body in motion is revolutionary, and seems contrary to all experience. It says that if an automobile is travelling at sixty miles an hour, with the engine turned off, it will continue travellling in a straight line at sixty miles an hour forever, unless some force is applied to it to stop it. The force which stops it is, of course, friction. If there were no friction, the car would never stop.
How did Galileo know, or "prove" this? How do we prove it now? The answer is that nobody can prove it. We have absolutely no experience of bodies moving without any force acting upon them. On the earth friction of some kind acts on all movmg bodies. It is true that if a stone is thrown along a sheet of ice it will travel much further than if it is thrown along a rough surface. This is sufficient to suggest Galileo's law, since it tends to show that the less friction there is the further the body will keep on
page 66
moving before it comes to a stop. But it is a bold and vast leap from this to the statement that with no friction at all it would keep on moving forever. No one could ever have any positive and decisive evidence of the truth of this because bodies moving without forces of some kind acting on them are unknown in our experience, and probably do not exist in the universe. For even the stars and planets are acted on by the force of gravitation.
Thus the law cannot be proved, but it is the simplest assumption we can make if we want, in a convenient manner, to predict physical motions. The case is the same here as with the "discovery" of Copernicus that the sun is the center of the solar system. There are various other assumptions about motion which you could make, and on the basis of which you could successfully explain all the observed phenomena of motion. You could make the common-sense assumption that bodies slow down and stop if no force acts upon them. Or you could assume that bodies acted on by no force will go on moving forever, but that their paths will be circular. You would then have to make suitable assumptions about the forces, for instance, that if a body is moving in a straight line a force must be acting on it to pull it out of its circular path. But if you make any assumption other than Galileo's, you will have to rewrite the science of mechanics in very elaborate and troublesome ways.
The special way in which the first law of motion became important in astronomy is that it enabled scientists to explain planetary and other celestial motions without assuming either the spirits or angels of popular thought or the whirlpools of Descartes.
This brings us to Newton (1642-1727). Newton was the great genius who completed the work of the foundation of modern science. He stood on the shoulders of Copernicus, Tycho Brahe, Kepler, and Galileo, and he could not have done his great work without them. But he brought to a conclusion the revolution in scientific outlook which they began. His contributions to science, apart from his discovery of the law of gravitation, were enormous. But here we shall have to ignore everything except the law of gravitation.
page 67
The point to note is that the assumption of the first law of motion abolishes the necessity of supposing that there must be a tangential force pushing or pulling the planets along their paths. Newton began his work by trying to explain the revolution of the moon around the earth, and only later applied the same explanation to the revolution of the planets round the sun.
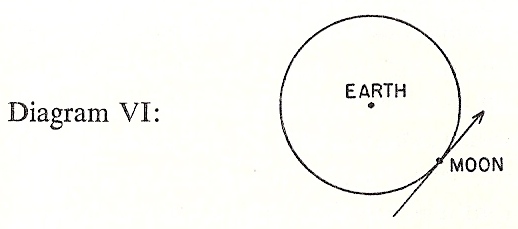
The theory that spirits push the planets and their satellites, and Descartes' theory of whirlpools, however we may consider the former more superstitious and the latter more scientific in spirit, were exactly alike so far as their mechanics were concerned. Both the spirits and the whirlpools exert forces acting along the tangent. The direction of the force must of course keep changing from point to point on the orbit in order to push the planets around instead of in a straight hne, but it will always be along the tangent. But now if we assume, as the first law of motion does, that the moon would, if no force at all acted on it, go on moving forever at the same speed in the straight line represented by the arrow in the above figure, then we see that the only thing required to make it move round and round the earth will be a force actmg along the radius from the moon to the center of its orbit, the earth.

No tangential force is necessary, since the moon's everlasting motion is explained without any forces, and the only thing which
page 68
requires a force to explain it is the change of direction from the straight line.
Newton, perceiving this, could dispense with all tangential forces, and look for a radial force. That this force was gravitation was by no means at once obvious, and to identify it as gravitation required great imaginative genius. It was not that the idea of gravitation was wholly new. Gilbert had already suggested that the earth is a magnet. Kepler had believed that the planets are moved by some power emanating from the sun. In any case gravitation was already known as a force acting towards the center of the earth. Apples fall from trees. But how far out into space does the gravitational force of the earth extend? If you ascend a mile in a balloon, you know that it is still exerting its influence, because if you throw something out of the balloon it falls to the ground. And bodies carried to the top of a mountain are still heavy. But as a matter of fact, as you ascend higher, the force of gravitation grows less and less, as is shown by the fact that a body at the top of a mountain weighs less than it does at sea-level. How can you be sure that the force does not fade out altogether at some point between the earth and the moon? How can you be sure that the moon, like the apple, tends to fall to the earth, and is only prevented from doing so by the outward pull of its own centrifugal force as it whirls round in its orbit?
There can be no direct evidence of this since no one can travel to a point halfway to the moon to see whether objects at that distance still tend to fall back to the earth. Newton therefore could not prove it, nor can anyone now. He just took it as an hypothesis and endeavored to see whether by this hypothesis he could explain the facts of the moon's motion. He made another guess. If the moon tends to fall to the earth, the only thing which keeps it from doing so must be its centrifugal force. And in order to keep it in its orbit the earth's attractive force must be equal and opposite to the centrifugal force. Some work had already been done on centrifugal forces by Huyghens, and Newton made use of this. Putting everything together he tried out the hypothesis—which subsequently, when it was found to work, was named the
THE RISE OF MODERN SCIENCE 69
law of gravitation—that the gravitational force between any two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. For the sake of shortness we may call this the law of the inverse square. In order to try this formula on the moon, he had to know its distance from the earth and the masses of the earth and the moon. He made use here of estimates which had already been made. His problem was to see whether, on these assumptions, he could mathematically calculate the motions of the moon so that the calculated motions would agree with the observed motions. To his great disgust he found that his attempt was a failure to the extent that there was a twelve per cent difference between the calculated motions and the actual motions. Newton, whether for this reason or some other, abandoned the problem for a long period. But when later it was found that the estimate of the distance of the moon from the earth which he had used in his calculations was in error, and a more accurate estimate was made, he took up the problem again. Using again the law of the inverse square, and the new estimate of the moon's distance, he recalculated the moon's motions, and this time his calculations agreed with the observed facts.
The rest of the story is brief in retrospect, though it involved immense labors. Newton found that he could explain the motions of the planets round the sun by the same law as explained the motion of the moon round the earth. Subsequent work showed that the law can successfully explain vast numbers of other pheenomena, for instance, those perturbations of the planets which are due to their gravitational forces acting on each other, and the phenomena of ocean tides. It was also found that the law can be extended beyond the solar system, and applies throughout space to all the stars. It thus became the universal law of gravitation. As is well known, Einstein has now substituted for it a more all-embracing law of gravitation. But that part of the story of science does not concern us in this book.
A further important point is that Kepler's three laws of planetary motion were shown to be consequences of the one law of
page 70
gravitation. That is to say, if you assume the law of gravitation, mathematical calculation will show that Kepler's three laws follow from it. They are not now "ultimate" laws as they seemed to be in Kepler's time. They have been "explained" by the law of gravitation. This throws light on the scientific concept of explanation. To explain a particular fact, such as the position of Jupiter in the sky at a given moment, means to show that it is a particular instance of some general principle or law, such as Kepler's laws. To explain the law itself means to show that it is a particular instance of some more general law. Thus Kepler's laws were proved to be particular cases of Newton's law, and Newton's law has now been shown to be a particular case of Einstein's law. How far explanation can go in this way we do not know. The ideal would be to show that everything which happens in the universe of whatever kind is finally to be explained in terms of one single ultimate law. No one knows whether this is even theoretically possible. And whether, if it were, one would have to say that the one ultimate law is itself "inexplicable" is a question which I leave to the reader to ponder.
A point of importance in regard to the relations between religion and science must here be noted. It was known to Newton that there are certain "irregularities" in the observed motions of the planets which he could not explain in terms of his law of gravitation. In other words, their actual motions diverged very slightly from what they should be as calculated by his law. Moreover if these irregularities were cumulative, they would in the course of time pile up to such great deviations that they would upset the whole balance of the solar system. The planets would either dive into the sun or break loose from its control and rush off into outer space. Why is it that this does not happen? Newton could think of only one explanation. It must be that from time to time God intervenes and puts the errant planets back on their proper paths. This is noteworthy as being, so far as I know, the last historical occasion on which a great scientist was willing to give supernatural mtervention as a cause of an observed phenomenon. The German philosopher Leibniz observed that Newton's God
page 71
was a mechanic, and a poor one at that, since he could only make a machine which coould be kept going right only by frequent subsequent tinkering.!
There is one other scientist whom I wish to mention here. Laplace (1749-1827) is not one of the founding fathers of sciience, and does not belong in the movement of thought which is commonly called the seventeenth century scientific revolution. He lived a century after Newton. Nor was he a scientific genius of the stature of Galileo or Newton. But he is of some importance in our story for reasons which will become evident in the next chapter.
Laplace showed that the irregularities in the movements of the planets which Newton was unable to explain by his law of gravitation are not cumulative, as Newton had supposed, but are self-correcting. Over a long enough period they cancel each other out. Therefore it is not necessary to introduce God to correct them.
Laplace was also one of the originators—Immanuel Kant being the other—of the famous nebular hypothesis for explaining the origin of the solar system. This was very influential in its time, although it is no longer accepted by astronomers. According to this hypothesis, the solar system was the offspring of a whirling nebula of incandescent gases. As the nebula cooled down, it contracted towards its center which became the sun. But in the dwindling process concentric rings of gas were left behind, and these rings, further cooling down, contracted into solid lumps which became the planets.
Now Newton had supposed that God created the solar system and set the planets and their satellites revolving round the sun with their proper speeds and motions in their proper orbits. The masses, distances, and velocities must all have been perfectly calculated by a mind "very well skilled in mechanics and geometry" so as to keep the machine running perfectly. If the earth had moved much more slowly than it does, it would have followed an orbit so eccentric that life on it would have been impossible; and if it had moved sufficiently slowly it would have collided with
page 72
the sun. If it had moved much faster than its present speed, it would have rushed off into outer space. If the distance between the earth and the sun had been much greater or less than it is similar results would have ensued. The same things would be true of the other planets and satellites. The distances and velocities of all these bodies must all have been calculated so as to keep the celestial machine in perfect balance—except for the unfortunate and unaccountable "irregularities." Laplace gleefully pointed out that just as God was not necessary to correct the irregularities, so he was not necessary to create the solar system, since its origin was now explained by the nebular hypothesis. It is related that Napoleon said to him: "I understand, M. Laplace, that you have wntten a great book on the system of the universe, and have never even mentioned its Creator"; and that Laplace replied: "I have no need of that hypothesis."
The comment of a theist will be, of course, that even if the nebular hypothesis were true, it would in no way do away with the necessity for God as a creator. It only pushes the necessity back a step. Presumably God created the nebula which caused the solar system. Or perhaps he created something which caused the nebula which caused the solar system. If a creating mind is necessary at the beginning, it does not matter how many phases of the universe have intervened between the creation and the present time. That criticism of Laplace, however, makes another story. I am not now discussing the reasonableness of his views, but stating what they were. We shall see that they were to play an nnportant part in the development of the modern mind—a topic which we shall have to leave to the next chapter.



